Three.js-Galaxy Generator 만들기

January 05, 2025

Three.js journey 강의를 들으며, galaxy를 만들 수 있는 부분이 있어서 참고해서 개발하며 정리한 것을 기록해보려고 한다.

Galaxy generator

1. 맨 처음 galaxy 함수를 하나 만들고, galaxy생성에 필요한 parameter 객체를 하나 만든다.


const generateGalaxy = () =>
{
    
}

generateGalaxy()
const parameters = {}

2. geometry와 particles(점) 만들기

parameters의 count는 은하 내 별의 개수로 보면 된다.

const parameters = {}
parameters.count = 1000

`BufferGeometry로 은하의 기하학적 데이터를 생성`

BufferGeometry는 Three.js에서 3D 모델의 정점 데이터를 효율적으로 관리하기 위해 사용되는 객체이다.

    const geometry = new THREE.BufferGeometry()

`positions 배열을 생성`

const positions = new Float32Array(parameters.count * 3)

Float32Array는 3D 공간의 좌표 데이터를 저장하는 배열이다.
parameters.count * 3으로 배열 크기를 설정한다.
각 점은 x, y, z 세 좌표를 가지므로 count * 3 크기가 필요하다.

`포인트 좌표 계산 및 할당`

for(let i = 0; i < parameters.count; i++)
{
    const i3 = i * 3

    positions[i3] = (Math.random() - 0.5) * 3  // x
    positions[i3 + 1] = (Math.random() - 0.5) * 3 // y
    positions[i3 + 2] = (Math.random() - 0.5) * 3 // z
}

반복문(for)

parameters.count(1000번) 반복하여 각 점의 x, y, z 좌표를 계산한다.

Math.random()

Math.random()은 0과 1 사이의 랜덤 값을 반환한다. -0.5를 빼고 3을 곱하여 값의 범위를 -1.5 ~ 1.5로 설정한다.

좌표 계산

positions[i3]: x 좌표
positions[i3 + 1]: y 좌표
positions[i3 + 2]: z 좌표
=> 3D 공간에 무작위로 배치된 점의 위치를 설정한다.

왜 이런 방식을 사용할까?
Math.random()만 사용하면 점들이 0 ~ 1 사이에 분포하므로, 좌표의 중심이 0이 아니라 0.5가 된다.
-0.5를 빼면 좌표의 중심이 0으로 이동한다. 그리고 곱하기 연산(* 3)으로 점의 분포 범위를 조정하여 원하는 크기의 공간에 맞춘다.

`BufferGeometry에 좌표 데이터 설정`

geometry.setAttribute('position', new THREE.BufferAttribute(positions, 3))

BufferAttribute는 Float32Array를 기반으로 데이터를 관리한다.
positions 배열을 position 속성으로 설정하여 BufferGeometry에 정점 데이터를 추가한다
3은 각 점이 x, y, z 세 가지 좌표로 구성됨을 의미한다.

`PointsMaterial로 재질(Material) 생성`

const material = new THREE.PointsMaterial({
    size: parameters.size,
    sizeAttenuation: true,
    depthWrite: false,
    blending: THREE.AdditiveBlending
})

PointsMaterial란?
PointsMaterial은 3D 공간에서 점(point)을 렌더링하기 위한 재질이다. 이 재질은 각 점에 대한 시각적 속성을 정의한다. (크기, 색상, 투명도 등)

재질 속성 설명

size: parameters.size
점의 크기를 지정한다. parameters.size = 0.02로 설정되어 있으므로 각 점이 작고 세밀하게 보이게 만든다.
sizeAttenuation: true
점의 크기가 카메라의 거리에 따라 조정될지 여부를 설정한다. true로 설정하면, 카메라에서 멀어질수록 점이 작아지고, 가까울수록 커진다. (원근 효과)
depthWrite: false
점이 다른 객체와의 깊이(depth) 테스트에 영향을 주지 않도록 설정한다. 이는 반투명 효과와 빛나는 효과를 자연스럽게 표현하기 위함이다.
blending: THREE.AdditiveBlending
가산 혼합(Additive Blending)을 사용하여 점들이 겹칠 때 빛나는 효과를 만든다.
겹쳐진 점들의 색상이 더해져 밝아지는 효과를 만들어낸다.
은하처럼 빛이 쏟아지는 느낌을 준다.

`points로 점을 생성`

const points = new THREE.Points(geometry, material)
scene.add(points)

Points란?
Points는 Three.js에서 점 클라우드(point cloud)를 생성하는 데 사용되는 클래스이다.
기하학(geometry)과 재질(material)을 결합하여 점 데이터를 3D 공간에 표시한다.

geometry는 점들의 좌표 정보를 담고 있다.(이전 코드에서 생성한 BufferGeometry) 그리고 각 점의 위치를 정의한다.
material은 각 점이 화면에 어떻게 표시될지(크기, 색상, 투명도 등)를 정의한다.

3. 나선형 모양 만들기

Radius parameter만들기

parameters.radius = 5
const radius = Math.random() * parameters.radius

radius는 각 점(별)이 중심에서 얼마나 떨어져 있는지를 나타내는 거리 값이다.
parameters.radius는 설정 가능한 값으로, 은하의 최대 반지름을 정의한다. 이 값은 은하의 크기를 결정한다. 예를 들어, parameters.radius = 5라면 점들이 중심에서 0에서 5 사이의 거리 안에 위치하게 된다.

Math.random() * parameters.radius를 계산하면, 점 하나가 중심에서 떨어진 거리가 0에서 parameters.radius 사이의 랜덤 값으로 설정된다.

나선형은하의 Branch만들기

parameters.branches = 3
for(let i = 0; i < parameters.count; i++)
{
  const i3 = i * 3
  const radius = Math.random() * parameters.radius
  const branchAngle = (i % parameters.branches) / parameters.branches * Math.PI * 2

  positions[i3    ] = Math.cos(branchAngle) * radius
  positions[i3 + 1] = 0
  positions[i3 + 2] = Math.sin(branchAngle) * radius
}

branchAngle 계산

const branchAngle = (i % parameters.branches) / parameters.branches * Math.PI * 2

i % parameters.branches에서 i는 점의 인덱스이고, parameters.branches는 은하의 branch 갯수이다.
i % parameters.branches 값을 branch 개수로 나누어, 현재 점이 해당 branch에서 차지하는 상대적인 위치를 0에서 1 사이의 비율로 변환한다.
Math.PI * 2는 360도(2π 라디안)를 의미한다.
비율 값을 곱하면, 현재 점이 중심을 기준으로 몇 도(라디안)인지를 계산한다.
예를들어 parameters.branches = 3일 때,
i = 0 → branchAngle = 0 → 0도
i = 1 → branchAngle = (1/3) * 2π → 약 120도
i = 2 → branchAngle = (2/3) * 2π → 약 240도

Math.cos와 Math.sin의 역할

positions[i3    ] = Math.cos(branchAngle) * radius // x 좌표
positions[i3 + 1] = 0                              // y 좌표
positions[i3 + 2] = Math.sin(branchAngle) * radius // z 좌표

Math.cos는 주어진 각도에서 x축 방향의 값(코사인)을 반환한다.
Math.sin은 주어진 각도에서 z축 방향의 값(사인)을 반환한다.
이 두 값은 특정 각도에서 점의 x, z 좌표를 계산한다.
예) branchAngle = 0 → (x, z) = (1, 0) branchAngle = π/2 → (x, z) = (0, 1) branchAngle = π → (x, z) = (-1, 0)

radius를 곱하는 이유?
계산된 cos와 sin 값에 radius를 곱하면 점이 중심에서 얼마나 떨어져 있는지를 설정된다. 즉, 점이 중심에서 radius 거리만큼 떨어진 위치에 놓이게 된다.

위와 같이하면 다음과 같은 3개의 branch가 만들어진다.

나선형 은하에 spin effect주기

parameters.spin = 1
const spinAngle = radius * parameters.spin

parameters.spin은 은하 branch가 얼마나 많이 감길지를 결정하는 값이다.
값이 클수록 점이 더 많이 회전한다. 값이 음수이면 회전 방향이 반대가 된다. spinAngle 계산은 radius와 parameters.spin의 곱으로 계산된다. 점이 중심에서 멀어질수록(radius 증가) spinAngle 값이 더 커져, 점이 더 많이 회전하게 된다.

    positions[i3    ] = Math.cos(branchAngle + spinAngle) * radius
    positions[i3 + 1] = 0
    positions[i3 + 2] = Math.sin(branchAngle + spinAngle) * radius

기존에 branchAngle로 계산한 은하 branch의 기본 각도에 spinAngle을 추가한다.
결과적으로, 중심에서 가까운 점은 spinAngle 값이 작아서 거의 직선 형태를 유지한다. 중심에서 먼 점은 spinAngle 값이 커져 더 많이 회전하며 나선형 곡선 형태를 형성한다.

4. 별들을 random하게 배치하기

현재상태에서는 점들이 각 branch에 완벽히 정렬되어 있다. 점들이 너무 기계적으로 배치되어, 은하가 비현실적으로 보일 수 있다. 각 점의 위치에 랜덤한 요소(randomness)를 추가하여 더 현실적인 은하 형태를 만들 수 있다.

parameters.randomness = 0.2
const randomX = (Math.random() - 0.5) * parameters.randomness * radius
const randomY = (Math.random() - 0.5) * parameters.randomness * radius
const randomZ = (Math.random() - 0.5) * parameters.randomness * radius

나선형 은하의 점(particle)들을 랜덤하게 흩뿌리는 효과를 추가한다.
a. Math.random() - 0.5
-0.5를 빼서 결과를 -0.5에서 0.5 사이의 범위로 변환한다.랜덤 값을 중심을 기준으로 양방향으로 분포시키기 위해 사용한다.

b. parameters.randomness
랜덤 값의 크기를 조정하는 파라미터로 값이 클수록 점들이 더 많이 흩어지며, 은하가 더 불규칙하게 보인다.

c. * radius
점이 중심에서 멀어질수록 랜덤 값의 크기를 증가시킨다. 이는 은하 중심부에서는 점들이 더 집중되고, 외곽으로 갈수록 점들이 더 흩어지는 효과를 만든다.

x좌표 계산

positions[i3] = Math.cos(branchAngle + spinAngle) * radius + randomX

Math.cos(branchAngle + spinAngle) * radius는 기존의 은하 branch 상에서 점의 x 좌표로 점이 은하 branch의 곡선을 따르도록 설정한다.
+ randomX: 기존 좌표에 랜덤한 값을 더해 점의 위치를 약간 어긋나게 만든다.

y 좌표 계산

positions[i3 + 1] = randomY

기존 코드에서 y 좌표는 항상 0으로 설정되어 평면에 존재한다. 여기에 randomY를 더해 점들이 위아래로도 분포되도록 설정한다.

z 좌표 계산

  positions[i3 + 2] = Math.sin(branchAngle + spinAngle) * radius + randomZ

기존의 은하 팔(branch) 상에서 점의 z 좌표에 점이 은하 branch의 곡선을 따르도록 설정한다. 여기에 randomZ를 더해 점의 위치를 약간 어긋나게 만든다.

그럼 아래와 같이 나선형 모양 은하에 별들이 random하게 배치된다.

5. 은하의 별들이 더 자연스럽게 흩어지고, 일정한 패턴이 덜 보이게 만들기

좀 더 은하들이 흩어지고 자연스러운 은하로 보이게 하기 위해 코드를 수정해준다.

const randomX = Math.pow(Math.random(), parameters.randomnessPower) * (Math.random() < 0.5 ? 1 : -1) * parameters.randomness * radius
const randomY = Math.pow(Math.random(), parameters.randomnessPower) * (Math.random() < 0.5 ? 1 : -1) * parameters.randomness * radius
const randomZ = Math.pow(Math.random(), parameters.randomnessPower) * (Math.random() < 0.5 ? 1 : -1) * parameters.randomness * radius

a. parameters.randomnessPower
이 값이 클수록 (예: 2) 더 큰 값으로 위쪽으로 변하고, 값이 작을수록 (예: 0.5) 값이 평평하게 분포한다. 이를 통해 외곽의 별들이 더 퍼지게 하고, 중심부는 더 촘촘하게 유지할 수 있다.

b. 부호 반전
(Math.random() < 0.5 ? 1 : -1) 부호를 랜덤하게 바꿔 점이 양쪽으로 균등하게 퍼지게 만든다. 예를 들어, randomX가 음수일 때는 왼쪽으로, 양수일 때는 오른쪽으로 퍼지게 되며, 다른 두 좌표(randomY, randomZ)도 동일한 방식으로 적용된다.

이렇게 코드를 변경해주면, 아래와 같이 별들이 더 흩어지며 자연스러운 은하 형태를 만든다.

6. 은하에 색상 추가하기

parameters.insideColor = '#ff6030'
parameters.outsideColor = '#1b3984'

material = new THREE.PointsMaterial({
  size: parameters.size,
  sizeAttenuation: true,
  depthWrite: false,
  blending: THREE.AdditiveBlending,
  vertexColors: true
})

각 vertex마다 색을 주기 위해 vertexColors를 true로 준다.

const colorInside = new THREE.Color(parameters.insideColor)
const colorOutside = new THREE.Color(parameters.outsideColor)

중심에 가까운 별은 색이 insideColor에 가깝고, 중심에서 멀어질수록 점점 outsideColor로 변하는 효과를 주는 것이다.

const mixedColor = colorInside.clone()
mixedColor.lerp(colorOutside, radius / parameters.radius)

colorInside.clone() ?
colorInside를 복제하여 mixedColor를 만든다. clone()을 사용하여 원본 색을 그대로 유지하면서, 새로운 객체에서 혼합 작업을 할 수 있게 만드는 것이다.

mixedColor.lerp(colorOutside, radius / parameters.radius) ?
lerp()는 선형 보간(Linear Interpolation)을 사용하여 두 색상 사이의 혼합을 계산한다.

첫 번째 매개변수: colorOutside — 혼합될 목표 색상.
두 번째 매개변수: radius / parameters.radius — 혼합 정도를 결정하는 값으로, radius는 현재 별의 중심으로부터의 거리이고, parameters.radius는 전체 은하의 크기이다.

radius / parameters.radius가 0이면 색은 colorInside로 유지되고, 1이면 색은 colorOutside로 완전히 변한다.

colors[i3    ] = mixedColor.r
colors[i3 + 1] = mixedColor.g
colors[i3 + 2] = mixedColor.b

colors 배열은 각 별의 색상 정보를 담고 있으며, r, g, b는 각각 빨강, 초록, 파랑 색상의 값이다. mixedColor.r, mixedColor.g, mixedColor.b는 혼합된 색의 빨강, 초록, 파랑 값을 가져와 각 별의 색상 배열에 할당한다.

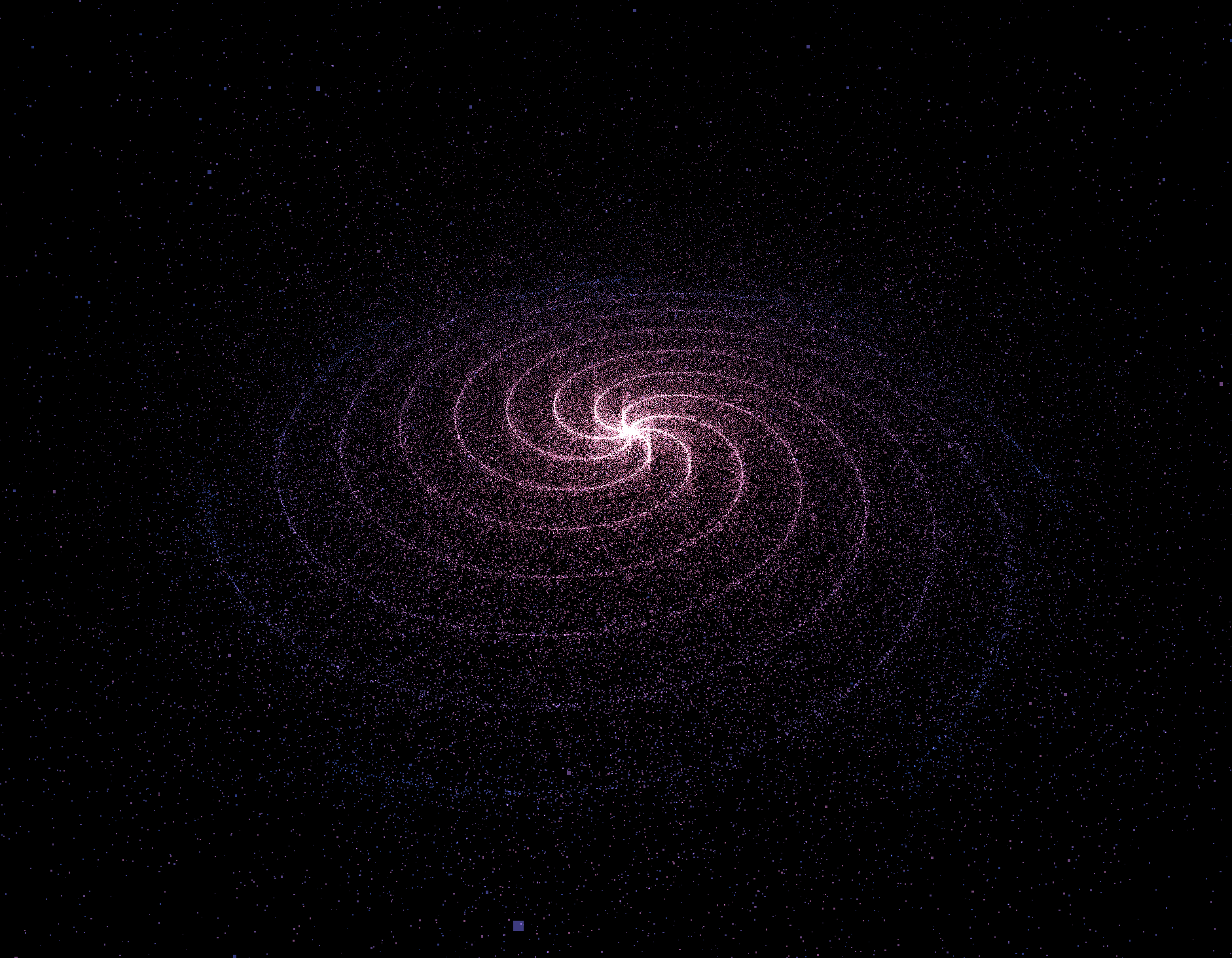
참고

Three.js journey

Written by@chloee

기록하는 것을 좋아하는 프론트엔드 개발자👩🏻‍💻

GitHub LinkedIn